半群:封闭性,结合律
monoid(幺半群):半群含单位元
循环群
a group of order n is cyclic if
and only if it contains an element of order n.
if p is prime, the
group $((\mathbb{Z}/p\mathbb{Z})^*,\cdot )$ is cyclic.
$\mathrm{Aut}(\mathbb{Z}/n\mathbb{Z})\cong ((\mathbb{Z}/n\mathbb{Z})^*,\cdot )$
The group $(\mathbb{Z}/n\mathbb{Z})^\times$ is cyclic if and only if n is $1,2,4,p^k,2p^k$ , where p is an odd prime and k > 0
Multiplicative group of integers modulo n;
群同态
Let ϕ : G → H be a group homomorphism, and let g ∈ G be an
element of finite order. Then |ϕ(g)| divides |g|.
群同构

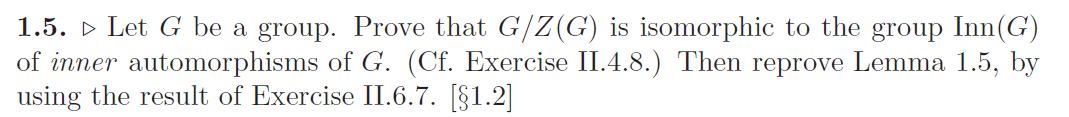
子群
子群的像,原像是子群
$\mathrm{ker},\mathrm{im}$是子群
$A\le C\Rightarrow AB\cap C=A(B\cap C)$
Sylow 子群
A subgroup of a finite group is termed a normal Sylow subgroup if it satisfies the following equivalent conditions:
- It is a Sylow subgroup, and is normal in the whole group.
- It is a Sylow subgroup, and is subnormal in + the whole group.
- It is a Sylow subgroup, and is characteristic in the whole group.
It is a Sylow subgroup, and is fully characteristic in the whole group.

正规闭包
$H\le G$,则$H$的正规闭包
即,包含$H$的最小的$G$的正规子群
子群的核
$H\le G$,则$H$在$G$中的核
积,包含在$H$中的极大正规子群
它$G$在$H$右陪集上的作用
的kernel
单群
可解群
$H\unlhd G,$则$G’\le H \Leftrightarrow G/H$交换
Lagerange’s theorem
The order |g| of any element g of a finite group G is a divisor of
|G|
If |G| is a prime integer p, then necessarily $G\cong \mathbb{Z}/n\mathbb{Z}$

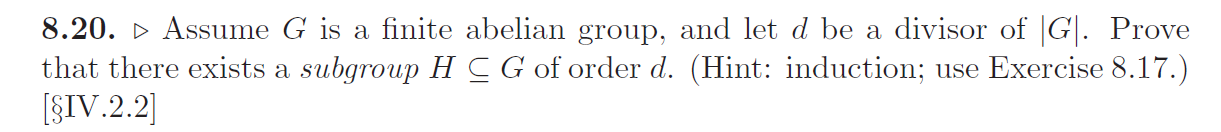
群构造
semidirect product

Proof:
(a)
It is sufficent to proof $H\cap N=1$Assume $x\in H\cap N$,then $|x|\big||H|$ and $|x|\big||N|$,but $(|H|,|N|)=1$,therefore $|x|=1\Rightarrow x=1\Rightarrow H\cap N=1$
(b)Since $|g(N)|=|N|$,
we will proof that the subgroup of order $|N|$ in is unique. Assume $H$ is a subgroup of order $|N|$,let $\overline{H}$ be the image of $H$ in $G/N$,that is,$\overline{H}=HN/N\simeq H/H\cap N$,therefore,$|\overline{H}|\big| |H|$ and $|\overline{H}|\big| |G/N|$,but $(|H|,|G/N|)=1$ ,we must have $\overline{H}=1$,that is $HN=N$,since $N\subseteq HN$,hence $H=N$.
Remark
According to the proof ,if $N$ is a normal group of $G$,and $(|N|,|G/N|)=1$,then $N$ is the characteristic subgroup of $G$,and such normal group is unique.And If $G$ has a group $H$ of order $|G/N|$,then the complement subgroup for $N$ exists,that is $G=HN$,and $G$ is the semidirect product of $N$ by $H$.If $|G/N|=p^r$ is a power of prime ,the Sylow theorem tells us such order of subgroup must exist, in such situation ,we call $N$ the normal p-complement of $G$,and we call G is p-nilpotent.If we have learned the Schur-Zassenhaus theorem,we will know that the $|G/N|$ order of subgroup always exists,or ,$N$ always has complement,and any two complemnt subgroup of $N$ are conjugated.
The conjugation action
